0. 출처
백준 2302번 문제입니다.
1. 문제
어떤 극장의 좌석은 한 줄로 되어 있으며 왼쪽부터 차례대로 1번부터 N번까지 번호가 매겨져 있다. 공연을 보러 온 사람들은 자기의 입장권에 표시되어 있는 좌석에 앉아야 한다. 예를 들어서, 입장권에 5번이 쓰여 있으면 5번 좌석에 앉아야 한다. 단, 자기의 바로 왼쪽 좌석 또는 바로 오른쪽 좌석으로는 자리를 옮길 수 있다. 예를 들어서, 7번 입장권을 가진 사람은 7번 좌석은 물론이고, 6번 좌석이나 8번 좌석에도 앉을 수 있다. 그러나 5번 좌석이나 9번 좌석에는 앉을 수 없다. 그런데 이 극장에는 “VIP 회원”들이 있다. 이 사람들은 반드시 자기 좌석에만 앉아야 하며 옆 좌석으로 자리를 옮길 수 없다. 오늘 공연은 입장권이 매진되어 1번 좌석부터 N번 좌석까지 모든 좌석이 다 팔렸다. VIP 회원들의 좌석 번호들이 주어졌을 때, 사람들이 좌석에 앉는 서로 다른 방법의 가짓수를 구하는 프로그램을 작성하시오. 예를 들어서, 그림과 같이 좌석이 9개이고, 4번 좌석과 7번 좌석이 VIP석인 경우에 <123456789>는 물론 가능한 배치이다. 또한 <213465789> <132465798> 도 가능한 배치이다. 그러나 <312456789> 와 <123546789> 는 허용되지 않는 배치 방법이다.

(1) 입력
첫째 줄에는 좌석의 개수 N이 입력된다. N은 1 이상 40 이하이다. 둘째 줄에는 고정석의 개수 M이 입력된다. M은 0 이상 N 이하이다. 다음 M 개의 줄에는 고정석의 번호가 작은 수부터 큰 수의 순서로 한 줄에 하나씩 입력된다.
(2) 출력
주어진 조건을 만족하면서 사람들이 좌석에 앉을 수 있는 방법의 가짓수를 출력한다. 방법의 가짓수는 2,000,000,000을 넘지 않는다. (2,000,000,000 < 231-1)
2. 문제 풀이
(1) 문제 풀이 방법
저는 DP를 활용해서 문제를 풀었습니다.
DP는 점화식이 중요하죠!
좌석이 여러 개 붙어있을 때의 경우의 수를 나열해 보면 다음과 같습니다.

이를 통해 dp[i] = dp[i-1] + dp[i-2] 인 것을 확인할 수 있습니다.
중간에 고정된 좌석이 있는 경우에는 증가하는 경우의 수가 중단되기 때문에 구역을 나누어 곱해주면 됩니다!
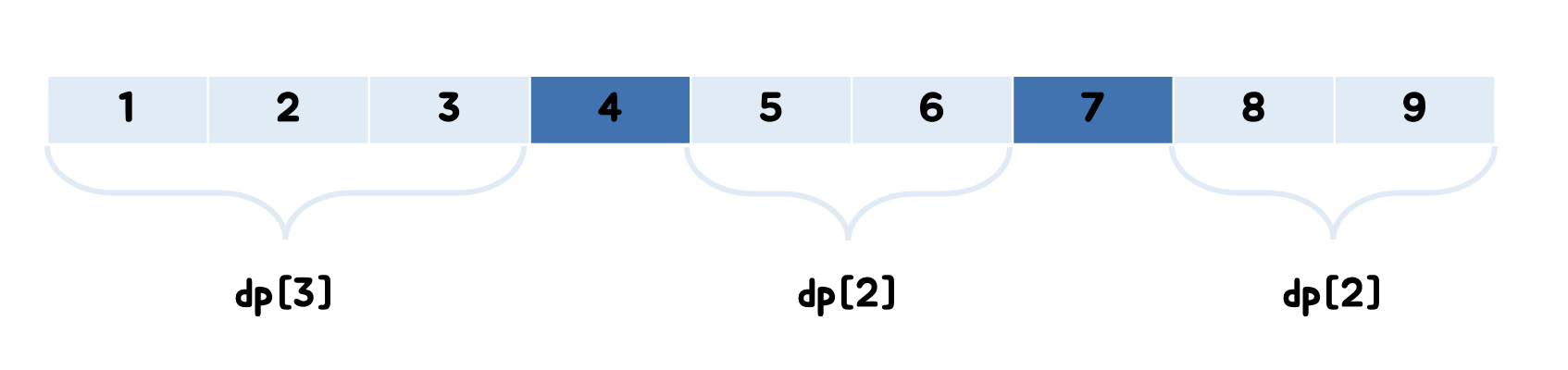
출력은 2,000,000,000을 넘지 않으므로 int형으로 처리해 주었습니다.
(2) 코드 (Java)
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int M = Integer.parseInt(br.readLine());
if(N == 1) {
System.out.println(1);
return;
}
int[] arr = new int[N+1];
for(int i=0; i<M; i++) {
int temp = Integer.parseInt(br.readLine());
arr[temp] = -1; // 고정석은 -1로 표시해 주었습니다.
}
int[] dp = new int[N+1];
dp[1] = 1;
dp[2] = 2;
for(int i=3; i<N+1; i++) {
dp[i] = dp[i-1] + dp[i-2];
}
int answer = 1;
int count = 0;
for(int i=1; i<N+1; i++) {
if(arr[i] == -1) { // 중간에 고정석이 있는 경우
if(count == 0) continue;
else {
answer *= dp[count]; // 전까지의 count 값을 곱합니다.
count = 0;
}
} else {
count++;
}
}
if(count != 0) {
// 마지막 좌석이 고정석이 아닌 경우를 고려해 마지막 count를 곱합니다.
answer *= dp[count];
}
System.out.println(answer);
br.close();
}
}
(3) 결과

'Algorithm & Data Structure > 코딩 테스트 문제풀이' 카테고리의 다른 글
| [백준] 1759번 암호 만들기 (Java) (0) | 2024.04.22 |
|---|---|
| [백준] 2529번 부등호 (Java) (0) | 2024.04.21 |
| [백준] 1347번 미로 만들기 (Java) (1) | 2024.04.19 |
| [백준] 1916번 최소비용 구하기 (Java) (2) | 2024.04.18 |
| [백준] 2157번 여행 (Java) (0) | 2024.04.17 |


댓글